算法-并查集

并查集

功能

• 将两个元素添加到一个集合中。
• 判断两个元素在不在同一个集合

常用场景

1. 判断图中的连通性：通过使用并查集，我们可以快速判断图中任意两个节点是否连通。首先，我们需要构建一个图的邻接表表示法，然后使用并查集来处理不相交节点的集合。如果两个节点属于同一个集合，则它们是连通的；否则，它们是不连通的。
2. 最小生成树问题：最小生成树问题是求解一个带权重的连通无环图的最小生成树。通过使用并查集，我们可以方便地处理带权重的边和顶点之间的关系，从而高效地求解最小生成树问题。
3. 网络连接问题：在网络连接问题中，我们需要判断两个节点之间是否存在路径或网络连接。通过使用并查集，我们可以快速判断两个节点是否连通，从而解决网络连接问题。

思想核心

维护一个数组：father[]数组，可以从树结构出发，理解为记录元素的父节点
维护四个函数：init()、find(int u)、isSame(int u, int v)、join()
代码模板

// 初始化father数组
int[] father = new int[n];

// 并查集初始化
public void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}
// 并查集里寻根的过程
public int find(int u) {
    return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}

// 判断 u 和 v是否找到同一个根
public boolean isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

// 将v->u 这条边加入并查集
public void join(int u, int v) {
    u = find(u); // 寻找u的根
    v = find(v); // 寻找v的根
    if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
    father[v] = u;
}

常见误区解释

误区：
由于isSame(int u, int v)和join(int u, int v)中的代码似乎重复了，就用改写如下：

// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

// 将v->u 这条边加入并查集
void join(int u, int v) {
    if (isSame(u, v)) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
    father[v] = u;
}

结论与反例：
首先给出结论，这样肯定不对，举出反例：

join(1, 2);
join(3, 2);
isSame(1, 3);    // 会发现结果是不一样的

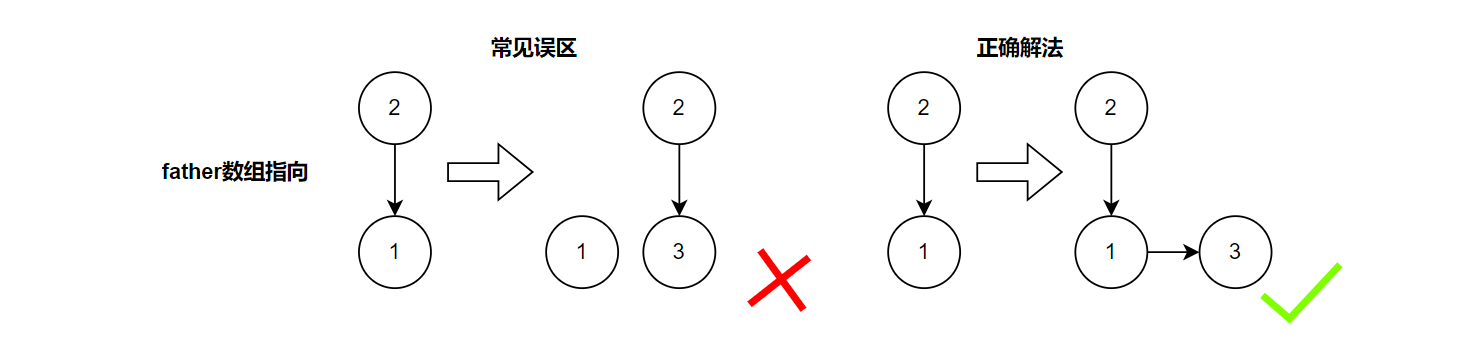
解释：
原因就发生在这两种不同的写法，在执行到father[v] = u;的时候，这个u是不一样的，在正确的写法中，这个u可能已经不是join(int u, int v)接收到的形参的值了；而错误写法中，u仍然是原来的值

public void join(int u, int v) {
    u = find(u); // 寻找u的根
    v = find(v); // 寻找v的根
    if (u == v) return ; 
    father[v] = u;          // 此时的u可能已经不是原来的u了，因为指向了原来u所指向的根
}