算法-KMP字符串匹配

介绍

KMP算法用途是进行字符串的匹配。

KMP算法相对于暴力算法有着较大的改进，主要是消除了主串指针的回溯（即主串只需要扫描一遍），从而使算法的效率有了某种程度的提高

**时间复杂度：O(n+m)**，n是主串的长度，m是模式串的长度

那么KMP算法是如何消除对主串的回溯的呢？

那么便需要理解KMP算法中的两个核心的东西：next[]数组（该数组由模式串决定），借助next[]数组 把 主串 和 模式串 进行匹配。

next[]数组

KMP算法的第一项工作便是求出next数组（换句话说就是，next[]数组是KMP算法得以进行的前提条件）。

作用

next[]数组的作用：万一模式串的某一个字符与主串匹配失败的时候，next[]数组对应下标的值可以指示模式串向右移动的步数（重点，作用理透了，next数组的底层原理，也就懂了一大半了）（参见下面的各变量的含义的“从全局上看”，两者是一个意思）

基本概念

在计算next数组之前，我们先理解几个next[]数组中所涉及到的概念：

• 前缀
• 后缀
• 最大公共前、后缀

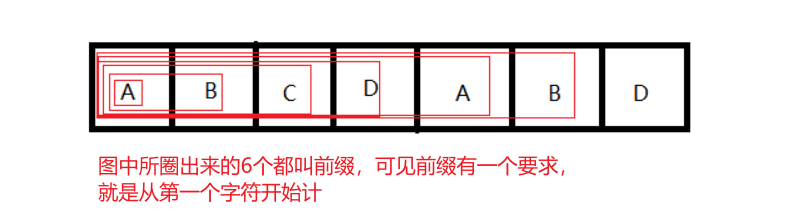
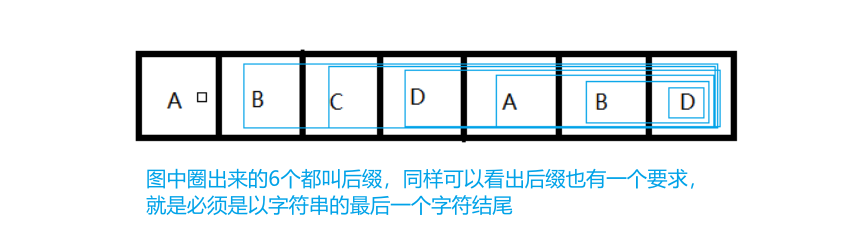
那么，最大公共前、后缀，理所当然就是指前缀、后缀中最大长度公共的辣！（可以轻松肉眼看出，上面字符串的最大公共前、后缀的长度为0，这算是当时设计的失误吧)

好了，基本概念讲到这就结束了。

计算next[]数组

在计算next[]数组的时候，有两种理解方式，但是这两种区别不大，分别是：

1. 模式串的下标为0的地方存储字符数据

   void Getnext(int next[],String t)
   {
      int j=0,k=-1;
      next[0]=-1;
      while(j<t.length-1)
      {
         if(k == -1 || t[j] == t[k])
         {
            j++;k++;
            next[j] = k;
         }
         else k = next[k];//此语句是这段代码最反人类的地方，如果你一下子就能看懂，那么请允许我称呼你一声大神！
      }
   }

2. 模式串的下标为0的地方不存储字符数据（本文采取这种，因为这种或许理解起来，更人性化一丢丢）（但是两种从本质上来讲，是一样的，理解了一种之后，在看另一种，也就懂了）

先放上代码（看不懂没关系，接着往后看讲解就行）：

//ch数组是模式串，length是模式串的长度，next数组就是我们所要求的next[]数组
void getnext(char ch[],int length, int next[])
{
    next[1] = 0;
    int i = 1, j = 0;
    while(i < length) {
        if(j == 0 || ch[i] == ch[j])
            next[++i] = ++j;
        else
            j = next[j];	//j回退
    }
}

首先我们要这段程序里，每个变量所代表的意思是什么？

各变量的含义

！一定要知道各变量的含义！

！一定要知道各变量的含义！

！一定要知道各变量的含义！

ch，length，next三个变量不再多说；

i，在本段代码中代表的是当前next已经计算到的位置（next[]数组是从0开始往右计算的）

j，在本单代码中表示的是对于每段字符串（对于整个模式串，会将其像前缀那样分解成一个一个小的字符串计算next数组）的前缀的最后一个字符的下一个位置（后面需要用到 j 的回退）

• 从全局看，next[]数组表示的是万一模式串的某一个字符与主串匹配失败时，所需要将模式串右移的步数；
• 从局部上看，j是next数组能够每一个值都计算正确（即某一个字符匹配失败的时候，能够将模式串右移正确的步数）的保障（因为j可以回退）

程序过程讲解

过程讲解主要抓住两点：条件+结果变化

起始值：j=0，i=1

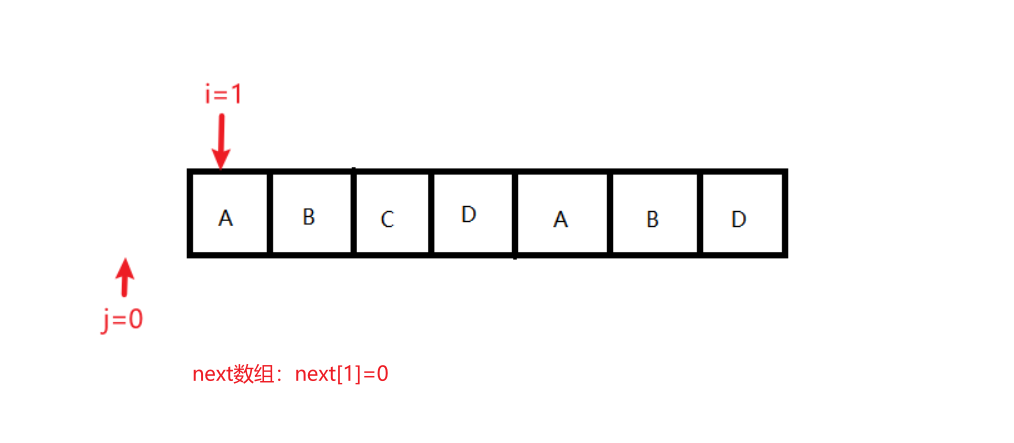
状态0：条件：j == 0；结果变化：next[++i] = ++j;，执行后，j = 1，i = 2，next[1]=0，next[2]=1

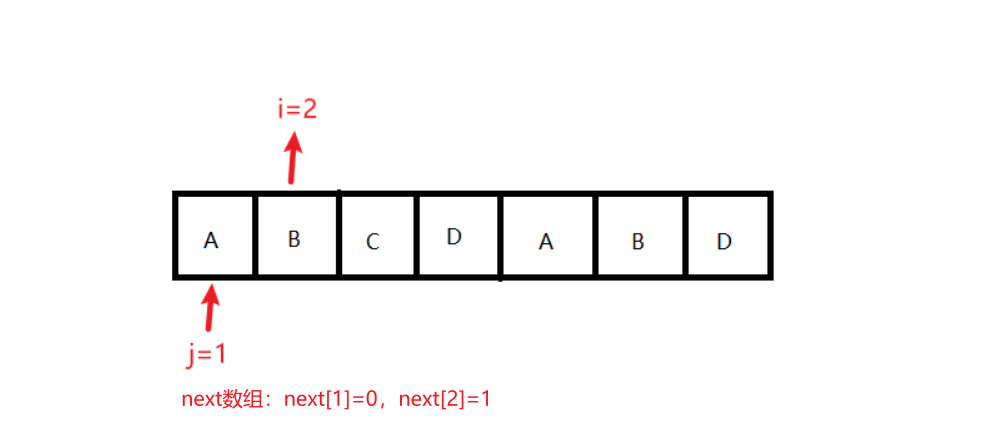
状态1：条件：j == 0 || ch[i] == ch[j]为假；结果变化：j = next[j]；执行后，j=0，i=2，next[1]=0，next[2]=1

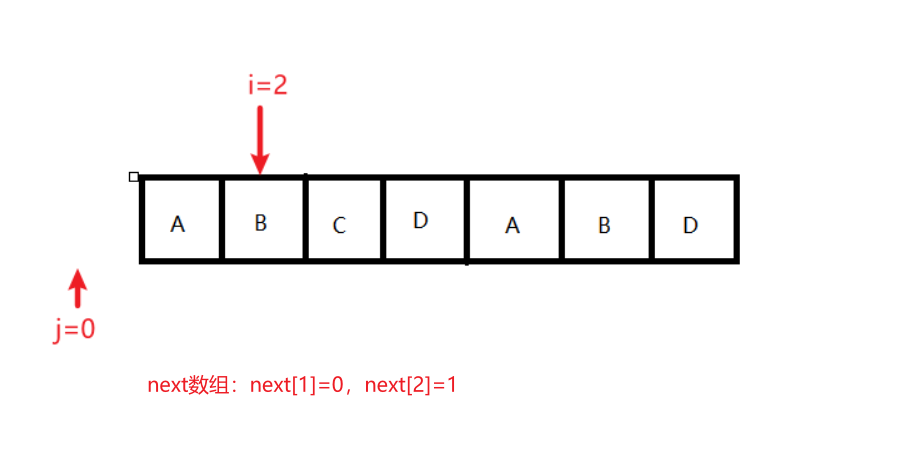
状态2：条件：j == 0；结果变化：next[++i] = ++j；执行后，j=1，i=3，next[1]=0，next[2]=1，next[3]=1

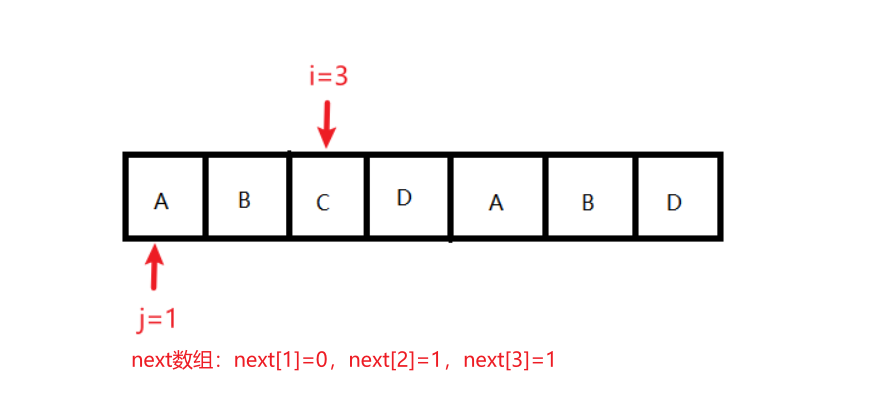
状态3：条件：j == 0 || ch[i] == ch[j]为假；结果变化：j = next[j]；执行后，j=0，i=3，next[1]=0，next[2]=1，next[3]=1

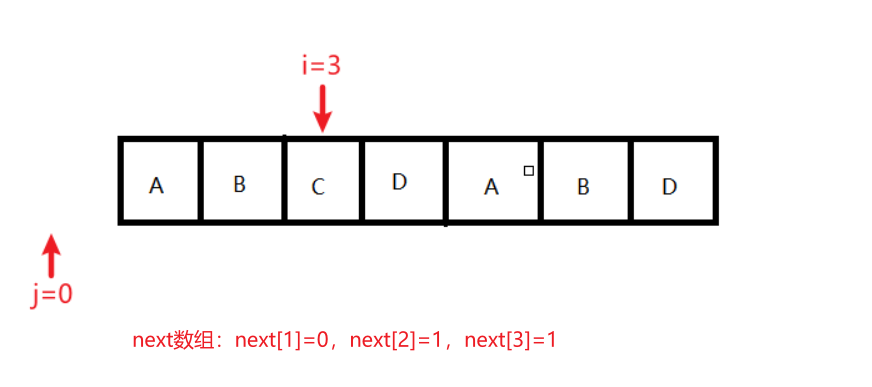
状态4：条件：j == 0；结果变化：next[++i] = ++j；执行后，j=1，i=4，next[1]=0，next[2]=1，next[3]=1，next[4]=1

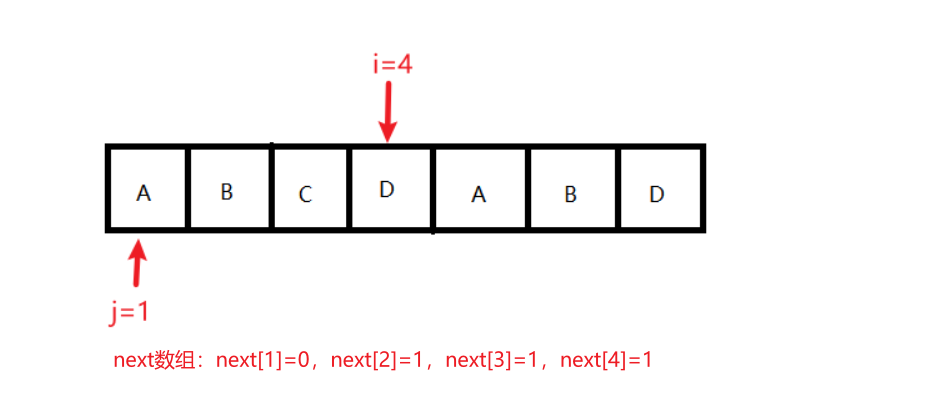
状态5：条件：j == 0 || ch[i] == ch[j]为假；结果变化：j = next[j]；执行后，j=0，i=4，next[1]=0，next[2]=1，next[3]=1，next[4]=1

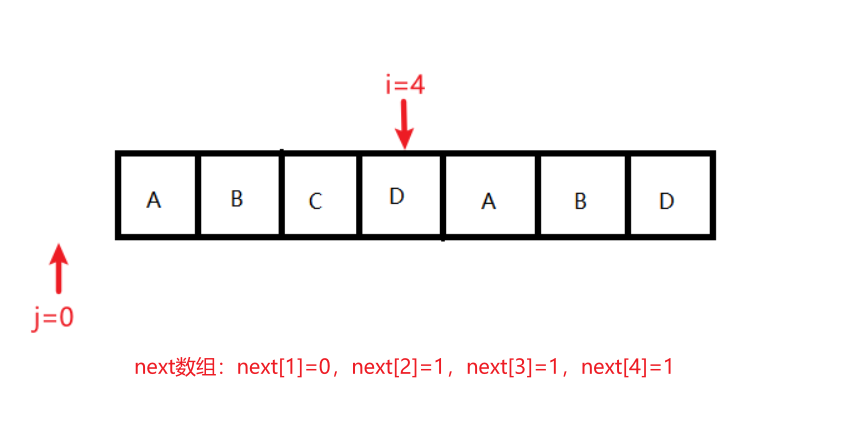
状态6：条件：j == 0；结果变化：next[++i] = ++j；执行后，j=1，i=5，next[1]=0，next[2]=1，next[3]=1，next[4]=1，next[5]=1

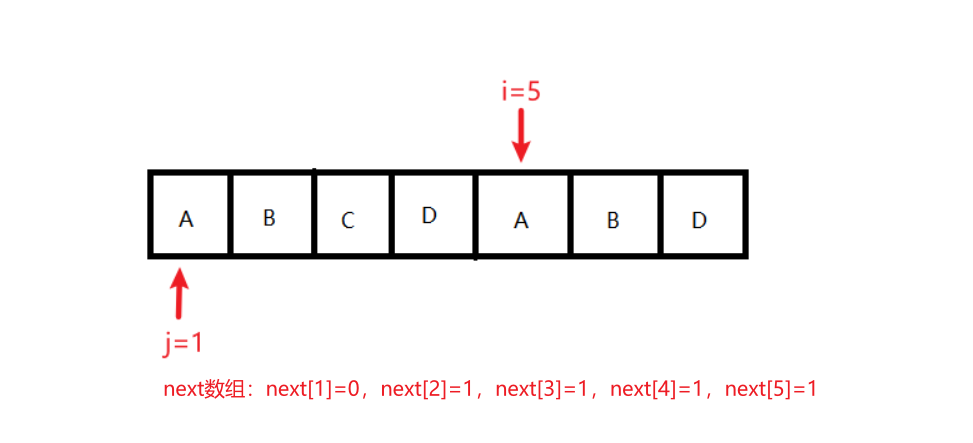
状态7：条件：ch[i] == ch[j]；结果变化：next[++i] = ++j；执行后，j=2，i=6，next[1]=0，next[2]=1，next[3]=1，next[4]=1，next[5]=1，next[6] =2

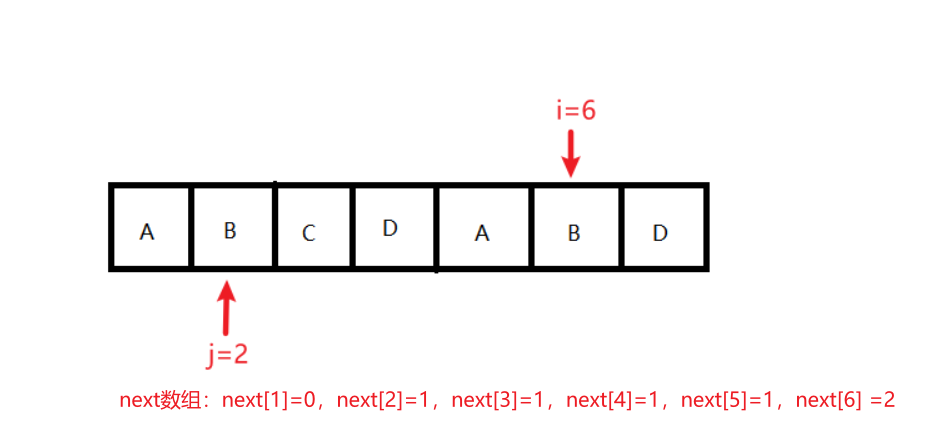
状态8：条件：ch[i] == ch[j]；结果变化：next[++i] = ++j；执行后，j=3，i=7，next[1]=0，next[2]=1，next[3]=1，next[4]=1，next[5]=1，next[6] =2，next[7]=3

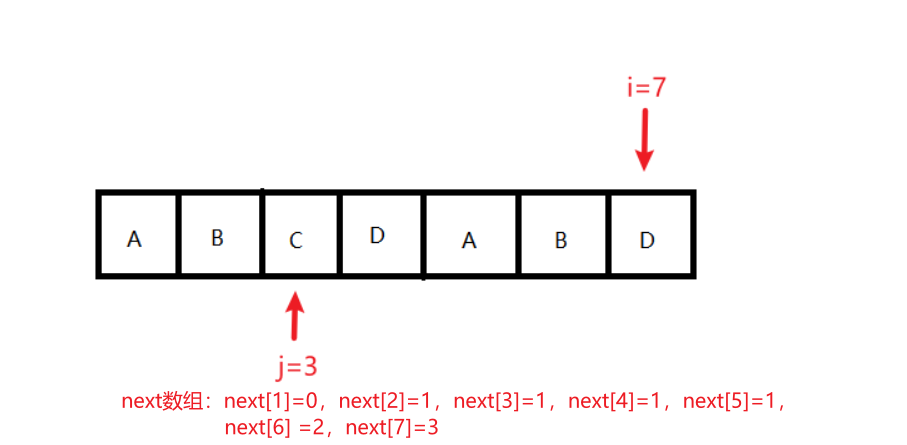
状态9：此时，条件：i < length已经不满足，所以跳出循环，此时next[]数组计算结束

next[]数组计算过程总结

经过上述的过程剖析，有这样几个发现：

1. 这里下标并没有用到0
2. i自始至终没有回退
3. j有回退，但是一直处于前缀当中

暂时可以下几个结论（同时也佐证了上面所讲的各变量的含义）：

1. next[k]的值是由前面k-1个字符所组成的字符串（不看k位置的字符）（确切的说，是前k-1个字符所组成的字符串的最大公共前、后缀的长度）决定的
2. j==0判断为真，的作用是为了让k处的字符匹配失败的时候，能够让下标为1处的字符与主串进行匹配

理解到这就是成功一大半啦！

KMP算法匹配

经过上面的步骤，我们现在已经有了next数组了。接下来只需要借助next数组进行模式串和主串匹配就可以了。

要想将主串和模式串进行比较，

因为next[]计算方式采取的是上面的第二种方式（即下标为0的位置不存储字符数据），所以KMP匹配算法也才去对应的下标为0的地方不存储字符数据。

上代码：

//s是主串，len1是主传的长度，p是模式串，len2是模式串的长度，next是求得的next[]数组 
//查询到了，就返回模式串在主串中的位置
//如果没有查询到，就返回-1
int kmp(char s[], int len1, char p[], int len2, int next[])
{
    int ret = -1;
    //这里i也可以为1，j也可以为1，这样就可以直接从下标为1的位置开始查询了
    int i = 0, j = 0;
    while (i <= len1)
    {
        //这里的j==0为真的时候，表示需要将模式串的第一个字符和主串的下一个字符进行匹配，所以需要进去执行i++, j++;
        if (j == 0 || s[i] == p[j])
        {
            i++, j++;
            if (j == len2)
            {
                //返回的是模式串在主串中的第一个字符出现的位置 
                return i + 1 - len2;
            }
        }
        else
        {
            j = next[j];
        }
    }
    return ret;
}

同样的方法，代码看不懂没关系，小的这就为您来讲解蛤(～￣▽￣)～

理解了上面的next数组的计算方法后，这个KMP匹配的过程就变得简单了。

案例：

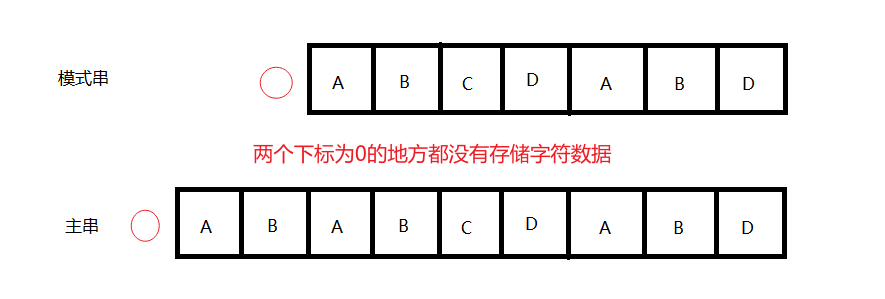
这里可以换一种理解方式，按照“条件 → 结果”的方式理解：

在匹配的过程中，会出现三种情况（条件）：

1. j回退到了0（回退是第3种情况的发生所导致的，看下面结果所采取的的措施就明白了）
2. s[i] == p[j]（即主串和模式串对应的字符相等）
3. 上述1和2两种情况都没有发生（即主串和模式串对应的字符不相等，且j不是0）

结果：

• 1和2都是需要将主串下一个字符与模式串 j+1 位置的字符进行比较的。
• 而第3种，就需要借助next[]数组，将 j 进行回退了，以便下次匹配的时候能够达到：既不需要回溯，又不会错过能够进行匹配的情况（不断提高了效率，还保证了正确性）

提供一个检测的算法正确性的例子

#include<iostream>
using namespace std;

//ch数组是模式串，length是模式串的长度，next数组就是我们所要求的next[]数组
void getnext(char ch[],int length, int next[])
{
    next[1] = 0;
    int i = 1, j = 0;
    while(i < length) {
        if(j == 0 || ch[i] == ch[j])
            next[++i] = ++j;
        else
            j = next[j];	//j回退
    }
}

//s是主串，len1是主传的长度，p是模式串，len2是模式串的长度，next是求得的next[]数组 
int kmp(char s[], int len1, char p[], int len2, int next[])
{
    int ret = -1;
    int i = 0, j = 0;
    while (i <= len1)
    {
        if (j == 0 || s[i] == p[j])
        {
            i++, j++;
            if (j == len2)
            {
                //返回的是模式串在主串中的第一个字符出现的位置 
                return i + 1 - len2;
            }
        }
        else
        {
            j = next[j];
        }
    }
    return ret;
}

int main(){
    //模式串 
    char a[] = {'1','A','B','C','D','A','B','D'};
    //主串 
    char b[] = {'1','J','K','A','B','C','D','A','B','D'};
    int length = 7;
    int next[8];
    //计算出next[]数组 
    getnext(a,length,next);

    printf("next数组对应的值（不包括下标为0的位置）：");
    for(int i = 1; i <= 7; i++){
        printf("%d\t",next[i]);
    }

    printf("\n\n返回查询结果");
    int result = kmp(b,9,a,7,next);
    printf("%d",result);	

    return 0;
} 

到这里就真的结束啦

总结

总的来说，KMP算法的核心，给我的感觉就是一个next[]数组，它能够让主串和模式串匹配时，在不回溯的情况下，还能保证不会漏掉一些可以进行匹配的情况。

需要重点学习的还是next[]数组的构造过程，next[]数组会构造以后，就可以自己借助next[]数组来完成KMP匹配算法的实现过程啦！